Tajomstvá utriedeného spájania, príbeh merge sortu

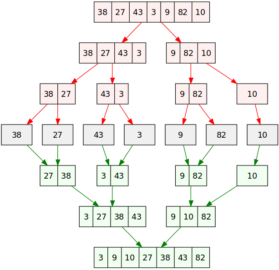
Merge sort je jeden z najefektívnejších triediacich algoritmov, má časovú zložitosť O(n log n). Jeho úspech spočíva v použití stratégie rozdeľovania a panovania. Jeho rekurzívna povaha a efektívna stratégia zlúčenia robia z neho efektívne riešenie pre triedenie veľkých dátových množín.

Postup algoritmu

1. Rozdeľovanie: Zoznam sa rozdelí na polovicu, a to opakovane, až kým nie sú vytvorené jednoprvkové podzoznamy.
2. Zlúčenie (Merge): Jednoprvkové podzoznamy sa zlúčia tak, aby vznikol nový zoznam. Pri tomto zlúčení sa zároveň zabezpečí, že prvky v novom zozname sú utriedené.

def merge_sort(zoznam):
     if len(zoznam) > 1:
         stred = len(zoznam) // 2  # celočíselné delenie
         lavy = zoznam[:stred]
         pravy = zoznam[stred:]
    
         merge_sort(lavy)
         merge_sort(pravy)

         zjednotenie_zoznamov(lavy, pravy)

1. Rozdeľovanie

merge_sort je rekurzívna funkcia, ktorá rozdeľuje zoznam a volá sa na oba vzniknuté podzoznamy.

2. Zjednotenie zoznamov

Funkcia zjednotenia zoznamov je kľúčovým prvkom v programe, ktorý zabezpečuje spojenie a zoradenie dvoch utriedených zoznamov. Využíva indexy pre postupné porovnávanie prvkov v oboch zoznamoch, pričom do výsledného zoznamu pridá ten menší z dvoch.

Verzia č. 1 funkcie pre zjednotenie zoznamov

def zjednotenie_zoznamov(zoznam1, zoznam2):
    # Inicializácia prázdneho výsledného zoznamu 
    # a indexov pre oba zoznamy
    vysledny_zoznam = []
    i = 0
    j = 0

    # zjednotenie zoznamov
    while i < len(zoznam1) and j < len(zoznam2):
        # Porovnanie prvkov na aktuálnych pozíciách v oboch zoznamoch
        if zoznam1[i] < zoznam2[j]:
            vysledny_zoznam.append(zoznam1[i])
            i += 1
        else:
            vysledny_zoznam.append(zoznam2[j])
            j += 1

    # Pridanie zvyšných prvkov z neukončených zoznamov
    while i < len(zoznam1):
        vysledny_zoznam.append(zoznam1[i])  ;  i += 1

    while j < len(zoznam2):
        vysledny_zoznam.append(zoznam2[j])  ;  j += 1

    return vysledny_zoznam

Verzia č. 2 funkcie pre zjednotenie zoznamov

def zjednotenie_zoznamov(zoznam1, zoznam2):
    # Inicializácia prázdneho výsledného zoznamu 
    # a indexov pre oba zoznamy
    vysledny_zoznam = []
    i = 0
    j = 0

    # While cyklus s podmienkou závislou od súčtu dĺžok oboch zoznamov
    while i < len(zoznam1) + len(zoznam2):
        # Porovnanie prvkov na aktuálnych pozíciách v oboch zoznamoch
        if i < len(zoznam1) and (j >= len(zoznam2) or zoznam1[i] < zoznam2[j]):
            vysledny_zoznam.append(zoznam1[i])
            i += 1
        else:
            vysledny_zoznam.append(zoznam2[j])
            j += 1

    return vysledny_zoznam

Časová zložitosť

Priemerný aj najhorší prípad má zložitosť O ( n log n ).

Keď delíme zoznam na polovicu, jeho veľkosť sa zredukuje na polovicu (n/2). Po ďalšom delení sa veľkosť zoznamu zredukuje na (n/2)/2= n/2², a tak ďalej. Počet delení potrebných na to, aby sme dosiahli zoznam veľkosti 1, je log₂ n. Preto je časová zložitosť rozdeľovania na polovicu O(log₂ n).

Časová zložitosť lúčenia je O ( n ), čo sa aplikuje pre každú rozdelenú časť, teda O ( log n ) x O ( n )